Wolfgang Amadeus Mozart, génie incontesté de la musique classique, n’a cessé de fasciner et d’intriguer depuis plus de deux siècles. Son talent précoce, sa créativité débordante, sa maîtrise parfaite des formes musicales en font une figure d’exception dans l’histoire de l’art. Mais saviez-vous que l’œuvre de Mozart recèle aussi un lien étonnant avec les mathématiques, et plus particulièrement avec le fameux nombre d’or ?
Le nombre d’or, souvent symbolisé par la lettre grecque phi (φ), est une proportion particulière, considérée depuis l’Antiquité comme esthétiquement idéale. Voici une rapide présentation mathématique (rassurez-vous, c’est à la portée de tous) :
Deux quantités sont dites en rapport de nombre d’or lorsque le rapport entre la plus grande et la plus petite est égal au rapport entre leur somme et la plus grande des deux. Autrement dit, si l’on a deux longueurs a et b, avec a >b, elles sont en proportion d’or si :
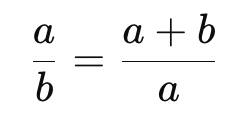
Cette relation implique que le rapport a / b est égal à un nombre spécifique, appelé nombre d’or et souvent noté ϕ, qui vaut environ 1,618.
Cette proportion remarquable se retrouve dans de nombreux phénomènes naturels, comme la spirale des coquillages ou l’arrangement des pétales des fleurs, mais aussi dans les arts, de la peinture à l’architecture.
Dans les années 1990, John Putz, mathématicien et musicologue, a étudié de près les sonates pour piano de Mozart pour y déceler la présence du nombre d’or. En analysant minutieusement la structure de ces œuvres, il a découvert que certaines proportions dans la répartition des mouvements, des mesures et des notes étaient étonnamment proches de ce nombre.
Par exemple, dans la Sonate n°1 en do majeur, si l’on considère la durée totale de l’œuvre, le second thème fait son apparition à un moment qui divise cette durée totale selon le nombre d’or. Autrement dit, le rapport entre la durée écoulée avant l’apparition du second thème et la durée restante après ce moment est très proche de 1,618.
De même, dans la Sonate n°16 en do majeur, la réexposition du premier mouvement (c’est-à-dire le retour du thème initial après le développement) intervient à un instant qui partage la durée du mouvement selon la proportion dorée.
Ces observations suggèrent que Mozart a pu, consciemment ou intuitivement, utiliser le nombre d’or pour structurer ses compositions et créer un équilibre harmonieux dans le déroulement de sa musique.
Ces découvertes ont suscité de nombreuses interprétations et spéculations. Mozart utilisait-il consciemment le nombre d’or dans ses compositions, ou était-ce le fruit du hasard ? Cette proportion mathématique serait-elle une clé universelle de l’esthétique musicale ? Ces analyses ouvrent en tout cas un pont fascinant entre musique et mathématiques, art et science. Elles suggèrent que la beauté et l’harmonie des sonates mozartiennes pourraient avoir une base rationnelle, une structure sous-jacente répondant à des lois mathématiques.
Cependant, il convient de rester prudent face à ces théories séduisantes. Le risque est grand de tomber dans la surinterprétation, de voir du nombre d’or partout, par un effet de biais de confirmation. D’autant qu’il est difficile de prouver une réelle intentionnalité de la part de Mozart. Rien ne dit qu’il avait connaissance du nombre d’or ou qu’il cherchait délibérément à l’intégrer dans ses compositions. Ces proportions harmonieuses pourraient tout aussi bien être le fruit de son intuition musicale, de son sens inné de l’équilibre et de la forme.
Il faut donc nuancer et contextualiser ces analyses, les voir comme des pistes de réflexion stimulantes plutôt que comme des vérités absolues. Elles nous invitent à considérer Mozart non seulement comme un compositeur inspiré, mais aussi comme un architecte du son, un bâtisseur de structures musicales d’une grande rigueur. Elles nous rappellent que la création artistique, loin d’être un pur jaillissement de l’esprit, peut aussi se nourrir de principes rationnels, de règles mathématiques, consciemment ou non.
